Primeiramente definimos o conceito de norma, sabemos que os elementos de um espaço vetorial são chamados de vetores e em certos espaços vetoriais podemos definir a norma. A norma nada mais é do que o "módulo" de um vetor, de forma técnica falamos que módulo aplica-se a escalares enquanto norma a vetores. No espaço usual (euclidiano) a norma é definida como o comprimento de um vetor.
Além disso, devemos saber o que é o espaço métrico. A métrica é definido como a distância entre dois pontos quaisquer, esta distância é o modulo da diferença de dois pontos, seja em dois ou tres dimensões.
Para 1 dimensão = |Ponto1 - Ponto2|
Para 2 dimensões = raiz( (pontoX1 - pontoY1)² + (pontoX2 - pontoY2)² )
Para 3 dimensões = raiz( (pontoX1 - pontoY1)² + (pontoX2 - pontoY2)² + (pontoX3 - pontoY3)² )
Sendo assim o nosso espaço euclidiano é um espaço métrico.
Quando a métrica de um espaço vetorial é induzido pela norma, ao invez do modulo, temos a definição de espaço normado.
Um espaço é dito completo se as series de Cauchy convergirem para qualquer valor de um elemento deste espaço, então este espaço é completo e se define a continuidade que implica em integração e derivação nesse espaço.
Além disso, temos a notação do produto interno. A norma é induzida pelo produto interno que por sua vez define a noção de distâncias e ângulos. Esquecendo um pouco da definição geométrica de distância e ângulo, os ângulos os quais iremos nos referir são abstratas e não tem como visualisar sua representação, entrando assim na álgebra abstrata, então podemos esquecer sobre representação geométrica, o espaço de Hilbert não tem geometria. No nosso espaço temos 3 dimensões, já no espaço de Hilbert tem infinitas.
O espaço de Hilbert é um espaço complexo, foi percebido que as função de onda e as transformações de Fourier possuem boas representações no espaço de Hilbert, então utlizar-se desse espaço na mecânica quântica é bem natural. Sabendo que o espaço de Hilbert é um espaço vetorial então cada ponto neste espaço será um vetor, sabemos também que as funções de onda representam os estados de uma partícula ou de um sistema, é muito comum utilizar-se a notação de Dirac, a notação Bra-Ket. O conjunto de todos os estados do sistema pode ser chamado de Ket e por estar em um espaço complexo o conjuntos de todos espaços conjugados é denotado por Bra.
O espaço de Hilbert tem algumas propriedades e são elas:
1) Um subespaço fechado do espaço de Hilbert tambem pertence ao espaço de Hilbert.
2) O produto interno é denotado da seguinte forma:
3) O produto interno induz a norma (a densidade de probabilidade)
4) Desigualdade de Cauchy-Schwarz
a desigualdade para ambas as funções forem antiparalelas e igualdade se foram paralelas.
5) < f | g > = < g | f >*
6) Duas funções não nulas são ortogonais se
< f | g >=0
7) A função é dita normalizada se tiver a norma igual a 1
|| f || = raiz( < f |f > ) = 1
8) Um conjunto de funções é dito ortonormal se os seus elementos são ortogonais entre si e sua norma ser 1
< f_i | f_j > = delta de Kronecker ={0 para i = j e 1 para i diferente de j}
A ortonormalidade é de extrema importância no espaço de Hilbert. Podemos ortonomalizar um conjunto qualquer de funções através do processo de Gram-Schmidt. O conceito de ortogonalidade tem relação com ângulo, mas como já dito antes, é uma definição abstrata de ângulo.
9) Um conjunto é dito completo se qualquer função do espaço de Hilbert pode ser escrita como uma combinação linear dessas funções do conjunto
Se o conjunto for ortonormal, podemos determinar os coeficientes
Cn = < f_n | g >
Operadores lineares são transformações que atuam em elementos do espaço de Hilbert e o resultado dessa ação é outro elemento do espaço. Dentro dos operadores do espaço de Hilbert nós temos, o operador adjunto, o operador simétrico (também chamado de hermitiano) e operador auto-adjunto.
O operador adjunto, também é chamado de conjugado Hermitiano do operador, sendo a notação (cruz) ao lado do operador.
O operador linear é dito hermitiano se o domínio deste operador for denso no espaço de Hilbert, e a seguinte igualdade for satisfeita
(Âf,g) = (f, Âg)
O operador é dito auto-adjunto se seguir algumas propriedades
1) todo autovalor de um operador auto-adjunto é real.
2) Se diferentes autofunções de um operador auto-adjunto são ortogonais.
Bom, isto sem duvidas foi um resumo do conteudo de cálculo bastante utilizado na mecânica quântica e que merece atenção.
Referências
- GRIFFITHS, D. J. Introduction to quantum mechanics. 2.e d., Prentice-Hall, 2005.

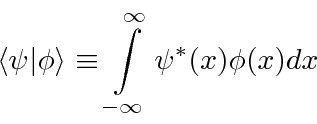
Nenhum comentário:
Postar um comentário